Echo Chamber: A Definition
According to the Cambridge Dictionary:
echo chamber (situation):
[/ˈek.əʊ ˌtʃeɪm.bər/]
A situation in which people only hear opinions of one type,
or opinions that are similar to their own.
Motivation
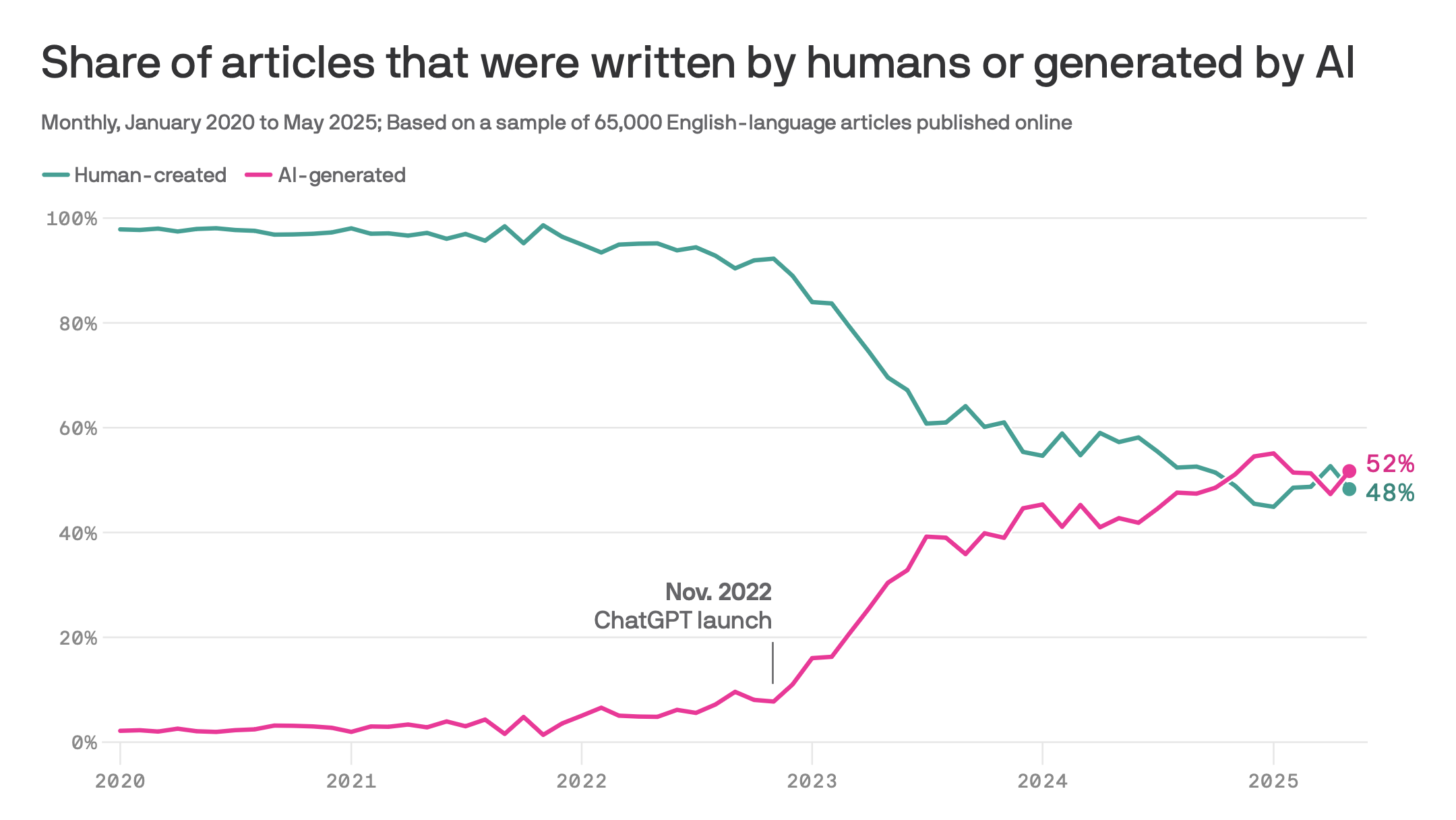
Source: Report from Graphite.io, Plot: Article by Axios.com
Online Learning
For
- Learner
- Nature (adversarial or stochastic) produces
- Learner suffers loss
Online Learning with a Replay Adversary
For
-
Learner
-
Nature (adversarial or stochastic) produces
-
Replay adversary reveals
-
Learner suffers loss
Online Learning with a Replay Adversary
Number of mistakes:
Replay adversary can pick
Define the reliable version space as the set of hypotheses consistent with all labels that could not have been produced by replay.
Related Work
- Online Learning: proper and improper learning, realisable and agnostic (different noise models)
- Closure Algorithm and Intersection Closed Classes
- Performative Prediction: learner's predictions induce concept drift
Example: Learning Thresholds
Consider
Halving-based Algorithm
Correct prediction
Example: Learning Thresholds
Consider
Halving-based Algorithm
Correct prediction
Halving-based Algorithm
Correct prediction
Define a Trap Region as a region where the leaner has predicted with both 0s and 1s in previous rounds, without being certain of the label.
Halving-based Algorithm
Correct prediction
Define a Trap Region as a region where the leaner has predicted with both 0s and 1s in previous rounds, without being certain of the label.
Halving-based Algorithm
Mistake?
Halving-based Algorithm
Mistake?
Closure-based Algorithm
Correct prediction
Closure-based Algorithm
Correct prediction
Closure-based Algorithm
Incorrect prediction: mistake
Closure-based Algorithm
Incorrect prediction: mistake
Closure-based Algorithm
Incorrect prediction: mistake
Insight: A closure-based algorithm never creates a Trap Region.
We show: For replay, only the closure-based algorithm achieves sublinear mistakes in
Closure-based Algorithm
Incorrect prediction: mistake
Insight: A closure-based algorithm never creates a Trap Region.
We show: For replay, only the closure-based algorithm achieves sublinear mistakes in
General Results: Prerequisites
- Define the
- For any
The
- Define the Threshold dimension as the largest
Definition
We define the Extended Threshold dimension of
where
Results on Extended Threshold dimension
For any hypothesis class
If
Furthermore, for every
Closure-Algorithm

Result I

For general convex bodies (